仮説検定では、いろいろ計算することによって、以下の二つの必ずどっちかが正しい!!と結論づける。
- 帰無仮説:μ=μ₀
- 対立仮説:μ=μ₁
↑いかなる場合でもどっちかが必ず真(と仮定)!どっちも正しい、とか、どっちも正しくないみたいな曖昧な結論は考えない。必ずどちらかが正しいという白黒はっきりさせるための検定。
まず、検定では以下のようなルールを作って、絶対に従う。
適当に確率変数が与えられた時、
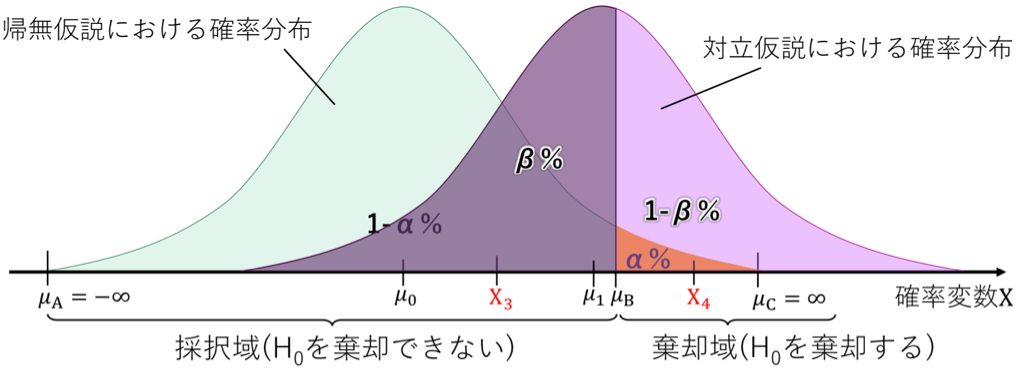
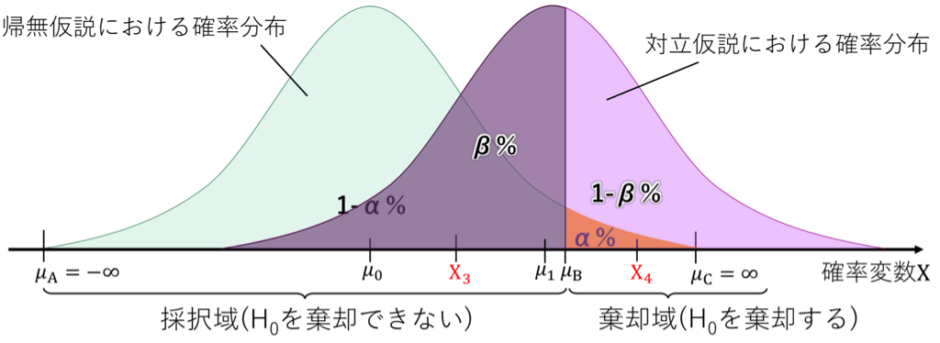
- μBより上(X₄)だったら「いやこの帰無仮説はおかしいやろ!(確率が低すぎるから)」と、絶対に帰無仮説を否定する。例えごく稀にそうなる確率があろうとも。
- μBより下(X₃)だったら「あ、帰無仮説正しいっすね。ごめんなさい。。」と素直に帰無仮説を真と認める。
検定は完璧ではない。二つの間違えかたがある。
確率変数がX4だったとしよう。検定によれば、帰無仮説は偽と判断することができる。
でももし、実は帰無仮説が正しいとしたら…
つまり、「流石に確率低すぎるからありえんやろ笑笑」と、すっぱり棄却したが、実はごく低い確率αで本当に帰無仮説が起こってしまったということだ。
これは第一の過誤である。そして、こう判断してしまう確率はαである。
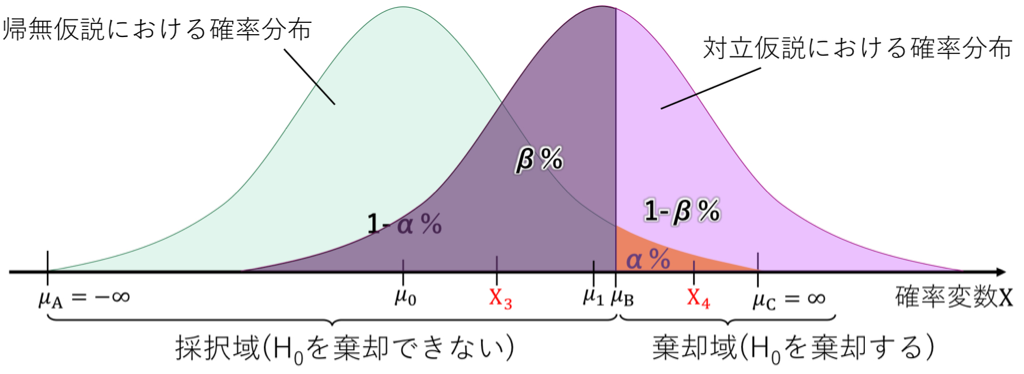
また、確率変数がX3だったとしよう。このとき、検定に従えば、「あー。これは帰無仮説は棄却できないねぇ…」と結論づけた。でも実は対立仮説が正しかった…。
帰無仮説を棄却しなかった結果、本当は対立仮説が真なのにそう判断できなかったということになる。
これを第二の過誤という。これが起こる確率はβである。
下の図だと結構大きいので、この検定は正直微妙だと言える。
- 第一の過誤:検定結果に従えば、帰無仮説(要するにマジのレアケース)を棄却してしまう確率。これは有意水準と同じになる。
- 第二の過誤:検定結果に従えば、対立仮説が正しいのに帰無仮説を棄却しないでおいてしまう確率。
μBが棄却域の下限である。二つの山の重なりが大きいほど、見分けが難しい。逆に、二つの山が離れてると正しく見分けられる確率が上がる。要するに検出力1-βが高くなる。
要するに、検出力(1-β)が大きければ第二の過誤は減らせる。
一方、1-α(信頼度)が大きければ、第一の過誤は減らせる
山のタイプを変えて、いろんな確率変数を取ってみて、いろいろ考察してみよう。