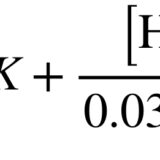酸は以下のような平衡状態にある。
HA ⇄ H + A
これより、平衡定数をK、pK=logKとすると
pH=pK+log([A]/[HA])
となる。この式をHenderson–Hasselbalch equationという。
さて、右の後に注目してほしい。もしAとHAの濃度が等しい場合、log1=0となる。
すると
pH=pK
となる。これは何を意味するかはグラフを描いたらわかる。
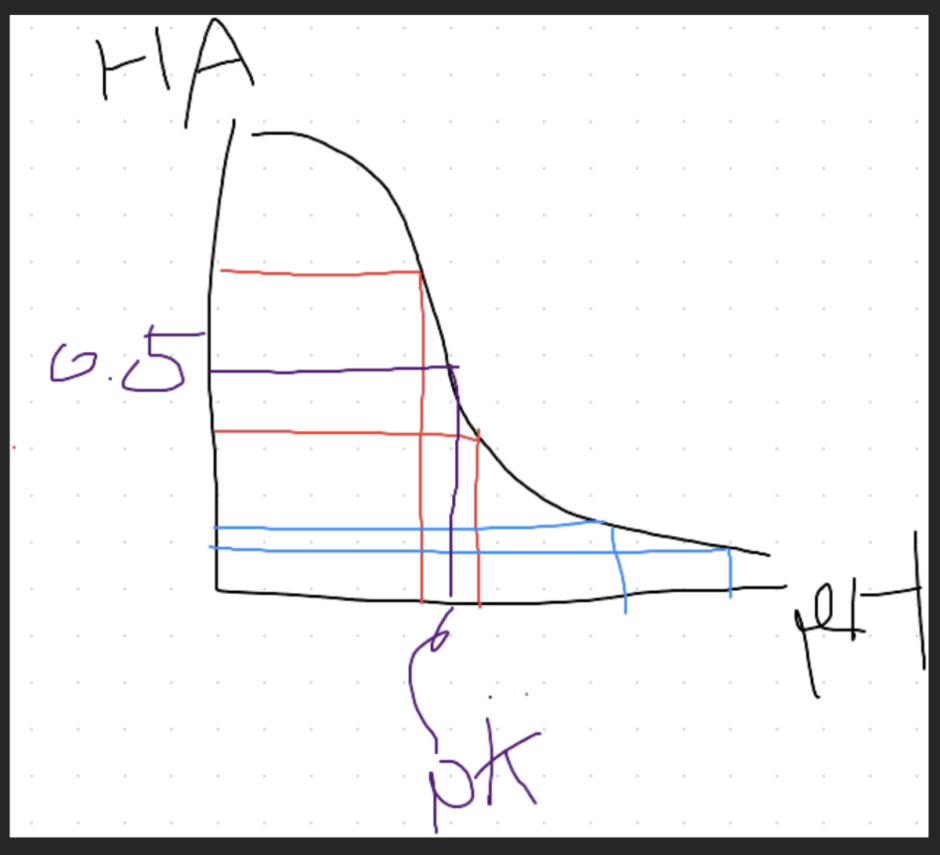
上の式を横軸pH、縦軸[HA]の相対濃度でグラフ化すると、
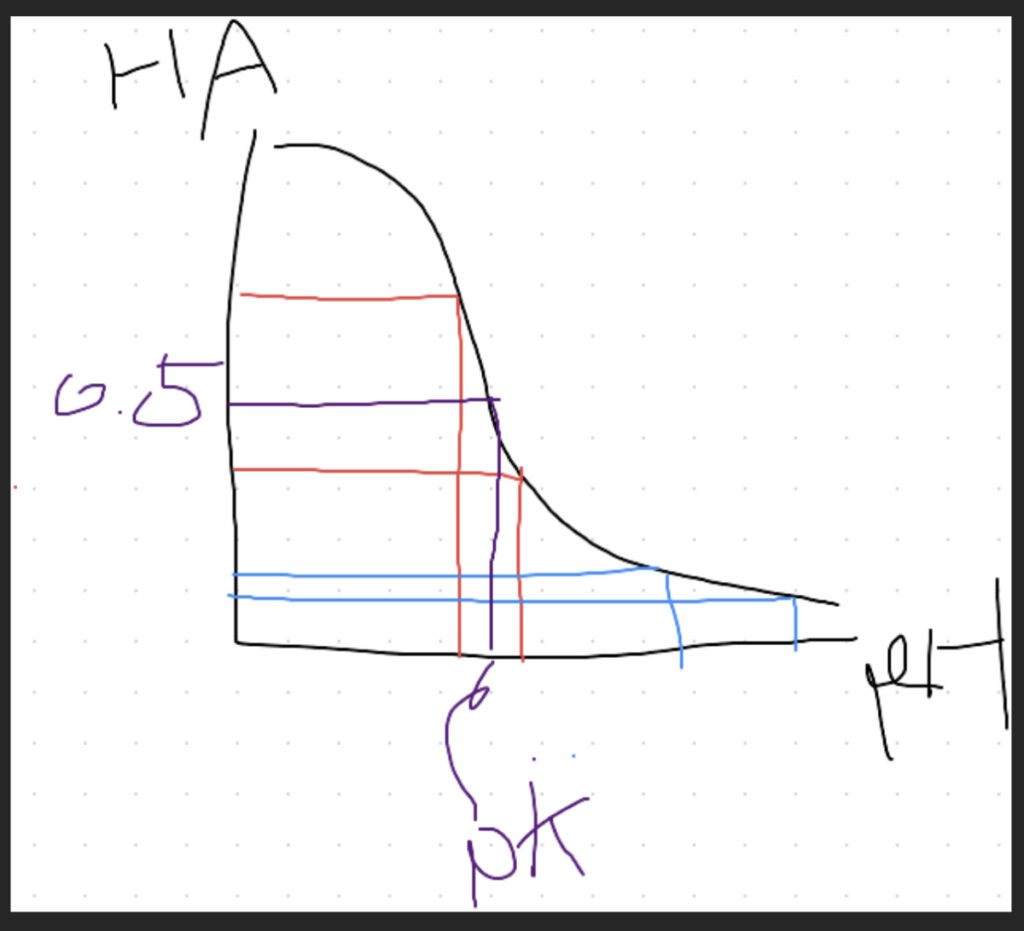
HAとAが等しくなる、つまりHAの相対濃度が0.5になる部分がpKということになる。
グラフの形上、赤の範囲内でHAが動いたときと、青の幅でHAが動いたときではpH変化が前者のほうが圧倒的に少ない。つまり、緩衝効果が高い。
もっと言えば、どんなグラフも縦が0.5付近ではこのような形状になる。
体内のpHを一定に保つ緩衝作用は当たり前だが、pH変化が少ないほうがいいに決まってる。
よって、体内のpHとその酸のpKが近いほど緩衝効果が高いということが言える。