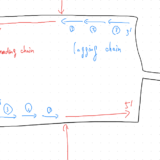
前提知識:遺伝子頻度
Aの遺伝子頻度:ある遺伝子Aの集団すべての中で発現している割合。つまり、AAの人が10人、Aaの人が10人、aaの人が10人なら、Aの遺伝子頻度は
(10×2+10)/30×2=0.5
となる。それぞれの人は対立遺伝子を二個ずつ持つので分母が2倍になるところは注意。
Hardy–Weinberg equilibrium
ハーディワインベルク平衡とは、ある集団において遺伝的減少を考察する上で、その集団にある一定の原則が成り立っていると仮定するものである。
簡単に言うと、超理想的な集団を仮定するってことですね。
その条件は次のようになる
- 無移動:集団内で人の流出や流入がない
- 無突然変異:遺伝子の突然変異によって新たな対立遺伝子mtが生まれることがない
- 任意交配:本当にランダムで結婚する
- 無選択:生存競争である対立遺伝子が不利になって淘汰されることがない
- 無限大:集団大きさが無限大であること。
さて、ハーディワインベルク平衡が成り立つそんな超理想的な集団ではAの遺伝子頻度p、aの遺伝子頻度qとすると、次世代は必ず
- AA:p²
- Aa:2pq
- aa:q²
となるようになっている。単純な確率と組み合わせで計算できる。これがHW平衡のメリットである。
逆に、ある集団がHW平衡を満たしていない限り、遺伝子頻度からこのような遺伝子型頻度を求めることはできない!!
例題(北海道大学医学部医学科 遺伝学 2014)

この集団ではHW平衡は成り立っているとは明記されていないので、くれぐれもq^2=36/400なんてことはしてはいけない。
遺伝子頻度は全体の割合から求める。
p=(76×2+88)/200×2=0.6

χ²検定についてはΧ二乗分布とΧ二乗検定で理解を深めてほしい。
ここでは簡単に計算方法を解説する。
確率変数χ²

はχ²分布に従うことがわかっている。
今回はこれを用いて仮説検定をすることにする。
帰無仮説:この集団はHW平衡に従っている
対立仮説:この集団はHW平衡に従っていない。
さて、帰無仮説が成り立っていると仮定した上で、AA、Aa、aaのそれぞれについて予測値を計算してみよう。
AAの遺伝子系頻度はp²となるはずなので、遺伝子型がAAとなる人は200×0.36=72人になると予想される。あくまでも予測されるだけ!!
Aa,aaも同様に、96,32とわかる。
さて、これと実測値を表にしてみると、以下のようになる
| expected | observed | |
| AA | 72 | 76 |
| Aa | 96 | 88 |
| aa | 32 | 36 |
これらのデータでχ²検定を行うと、確率変数χ²は
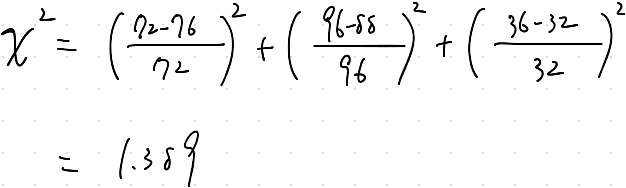
問題の条件より、
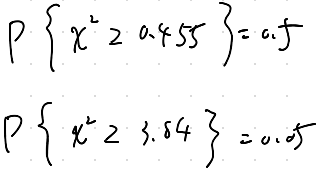
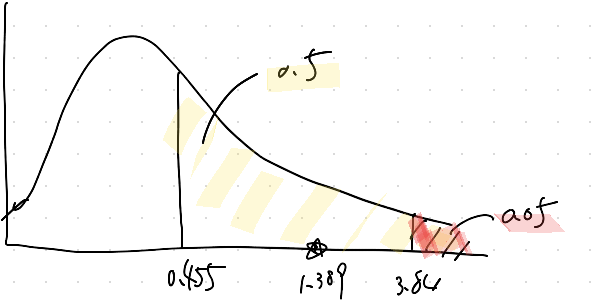
これより、1.389は棄却域には含まれないので、帰無仮説は棄却されない。
よって、この集団はHW平衡に従っているといえる。