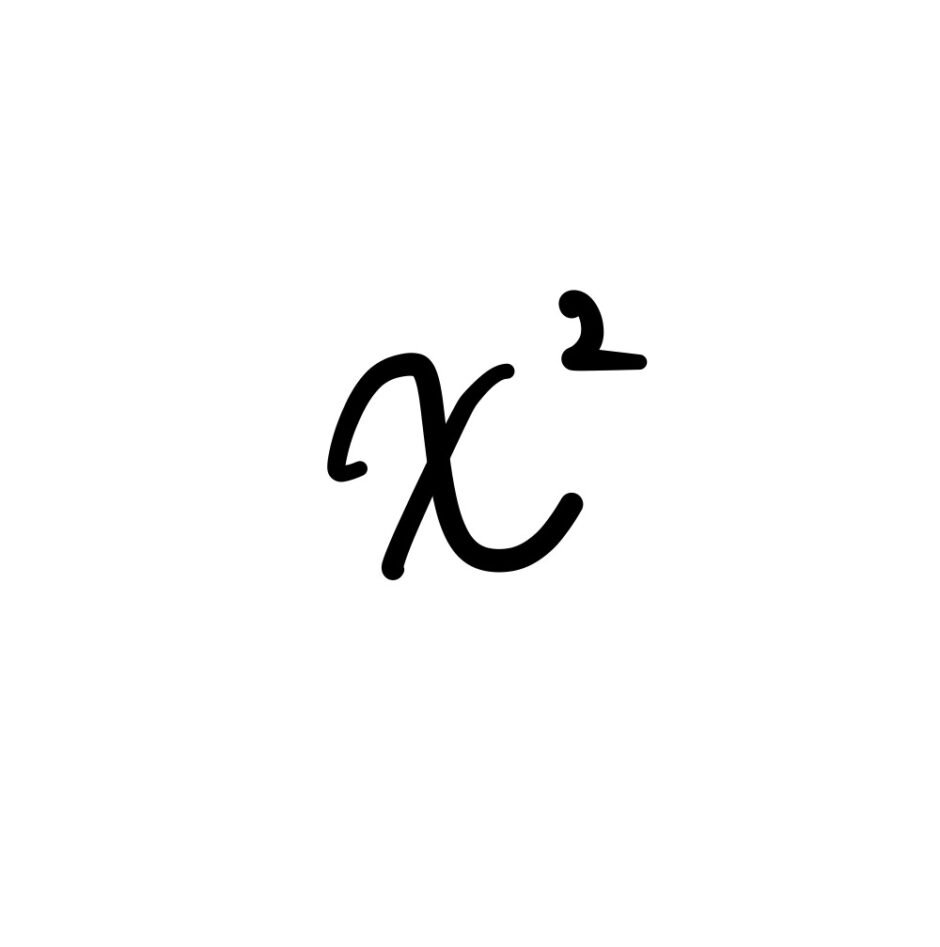χ二乗分布
標準正規分布N(0,1)に従うν(ニュー)個の無作為標本(Z₁~Zn)の二乗和
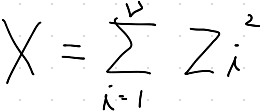
は自由度νのχ二乗分布に従う。確率密度関数のグラフは以下のようになる。
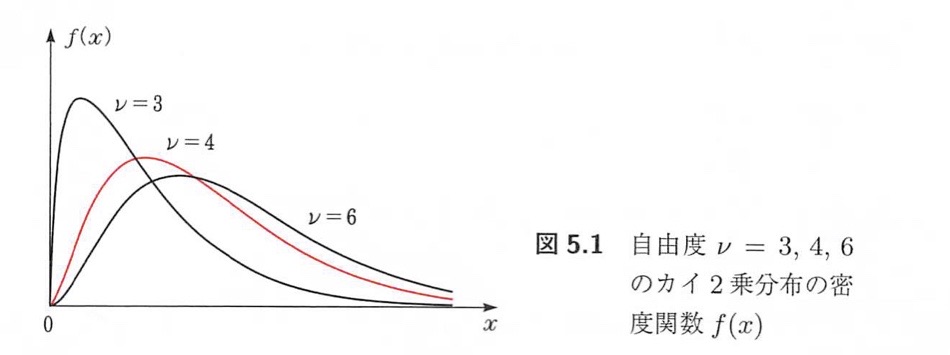
χ二乗検定
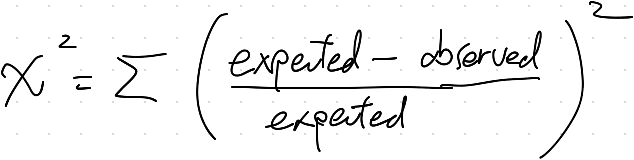
上の式で与えられる確率変数χ²について考えてみよう。ここまではまだχとか文字のことに関しては考えなくていい。ただ、予測値と観測値の誤差の二乗という何らかの変数が与えられてと思ってもらっていい。
もし観測したデータが予測値と近かったら,χ²はゼロに近づく。反対に観測したデータが予測値と大きくずれていた場合はχ²は大きくなるよね。
つまり、この確率変数χ²は予測値と実測値がどれだけ乖離しているかを表す指標になる!!!
なんと、このχ²という確率変数は、χ²分布に従うことがわかっている。よって、正規分布での検定のように、付表を使えばχ²分布でも検定を行うことができる。
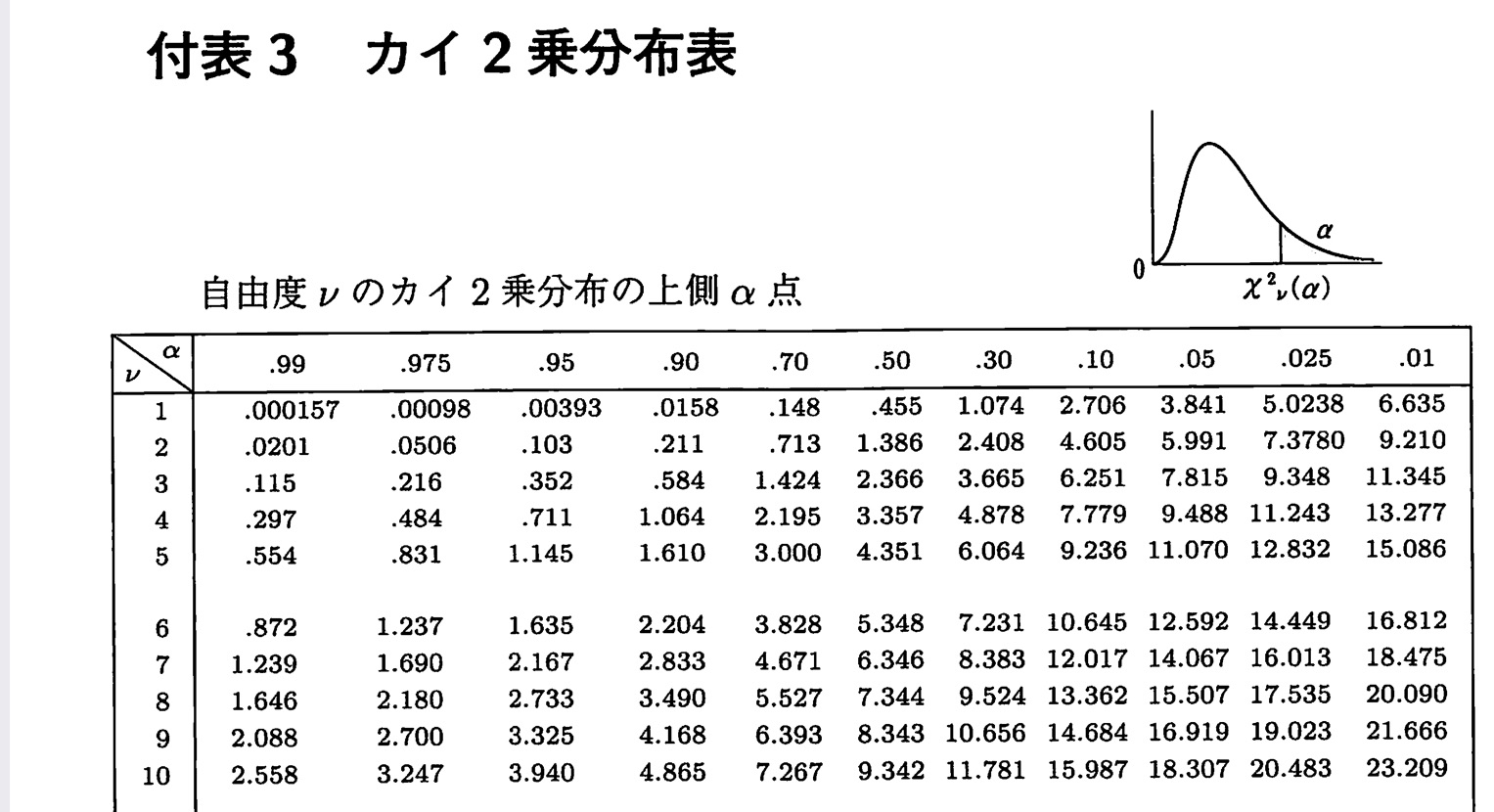
次の式の意味はわかるだろうか。ただし,自由度は1とする!!
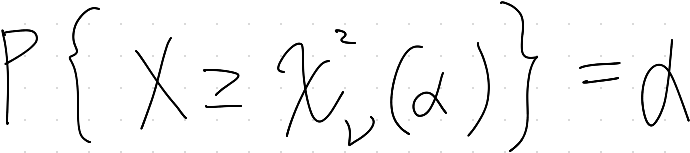
これは、確率変数Xがある値χ²(α)を超える確率がαであるという意味である。
もっとわかりやすくいうならば,

確率変数Xが0.455を超える確率は0.5ですよ。という意味になる。
つまり、χ²(α)は0.78のようなある決まった定数というふうに見られるようになろう。
有意水準を5%に設定すると
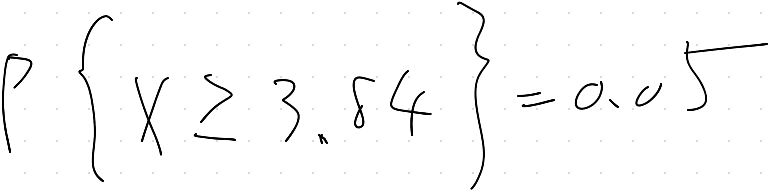
これを図示すると以下のようになる。
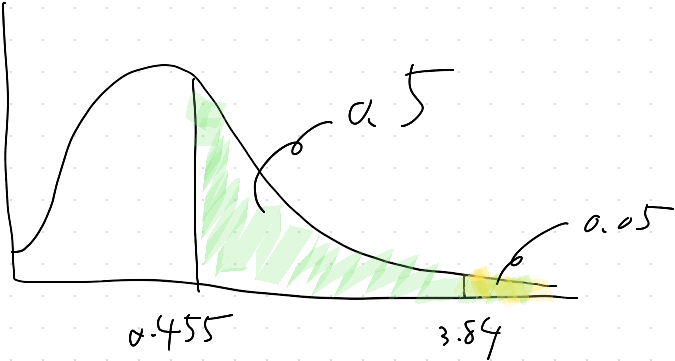
よって、χ²分布を用いた仮設検定で確率変数が3.84を超えたら、その帰無仮説は棄却される。
検定の仕方などについては実例を通して理解を深めほしい。